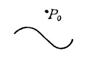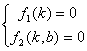十、微分的应用(I)— 函数的极值
1.单变量函数的极值
[极值(极大值或极小值)]若函数f (x)在点x0的双侧邻域中有定义,并且对于某邻域0<|x-x0|<δ内的一切点x,下面不等式成立:
f (x)< f (x0) (或f (x)> f (x0))
则称函数f (x)在点x0处有极大值(或极小值).
[极值存在的必要条件]假定函数f (x)在区间(a,b)内存在有限导数.若在点x0(∈(a,b))处函数有极值,则必有
![]() =0
(1)
=0
(1)
所以可微函数的极值只能在使(1)式成立的点达到,这种点称为稳定点.
[极值存在的充分条件]
第一法则 若函数f (x)满足条件:(i)在点x0的某邻域|x-x0|<δ内有定义并且连续,且在点x0处,![]() =0或不存在,(ii)在范围0<|x-x0|<δ内有有限的导数
=0或不存在,(ii)在范围0<|x-x0|<δ内有有限的导数![]() ,(iii)
,(iii)![]() 在点x0的左右两侧有固定的符号,则函数f (x)在点x0有无极值见下表:
在点x0的左右两侧有固定的符号,则函数f (x)在点x0有无极值见下表:
|
x |
x < x0 |
x 0 |
x> x0 |
f (x) |
|
|
+ — + — |
0 |
— + + — |
极大值 极小值 上升 下降 |
第二法则 若函数f (x)有二阶导数![]() ,并且在点x0处下列条件成立:
,并且在点x0处下列条件成立:
![]() =0及
=0及![]() ≠0
≠0
则函数f (x)在此点有极值,当![]() <0时,有极大值;当
<0时,有极大值;当![]() >0时,有极小值.
>0时,有极小值.
第三法则 设函数f (x)在某邻域|x-x0|<δ内有导数![]() ,
,![]() ,且
,且
![]() =0 (k=1,
=0 (k=1,![]() )
)
![]() ≠0
≠0
若n为偶数,则函数f (x)在点x0处有极值(当![]() <0时有极大值,当
<0时有极大值,当![]() >0时有极小值);若n为奇数,则在点x0处无极值.
>0时有极小值);若n为奇数,则在点x0处无极值.
以上介绍的单变量函数的极值求法中,求稳定点时最后都归结为求方程
![]() =0
=0
的实根.有时上述方程的实根不易求得,就要求近似根.关于实根的近似计算法可参考第三章,§4.
2.多变量函数的极值
[极值(极大值或极小值)] 设函数
y= f (x1,x2,![]() )= f (x)
)= f (x)
定义于区域D中,且x0=(![]() )是这区域内的一点.
)是这区域内的一点.
若点x0有一个邻域
0<|![]() |<δ,i=1,2,
|<δ,i=1,2,![]()
使对于其中一切点,下面不等式成立:
f (x)< f (x0) ( 或f (x)> f (x0))
则称函数f (x)在点x0处有极大值(或极小值).
[极值存在的必要条件] 假定函数f (x)在区域D内存在有限偏导数.若在点x0(∈D)处函数有极值,则必有
 (2)
(2)
所以极值只能在使(2)式成立的点达到,这种点称为稳定点.
[极值存在的充分条件(二元函数的情形)]
设点x0=(![]() )为函数y= f (x1,x2)的稳定点,并且函数f (x1,x2)在稳定点x0的邻域内有定义,连续,并有一阶及二阶连续偏导数.引进记号
)为函数y= f (x1,x2)的稳定点,并且函数f (x1,x2)在稳定点x0的邻域内有定义,连续,并有一阶及二阶连续偏导数.引进记号
![]()
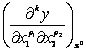 ,k = p1+p2
,k = p1+p2
上指标“0”表示偏导数是在x0计算的.记
D1=![]() ,D2=
,D2=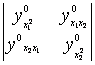
那末(i)稳定点x0是极小点的充分条件是:
D1>0 和 D2>0
即 ![]() >0 和
>0 和 ![]() >0
>0
(ii)稳定点x0是极大点的充分条件是:
D1<0 和 D2>0
即 ![]() <0 和
<0 和 ![]() >0
>0
若D2<0,则x0不是极值点,当D2=0时不能肯定x0是否极值点,必须考察更高阶的偏导数.
[极值存在的充分条件(一般情形)] 设点x0=(![]() )为函数y= f (x)= f (x1,x2,
)为函数y= f (x)= f (x1,x2,![]() )的稳定点,并且函数f (x)在稳定点x0的邻域内有定义,连续,并有一阶及二阶连续偏导数.引进记号
)的稳定点,并且函数f (x)在稳定点x0的邻域内有定义,连续,并有一阶及二阶连续偏导数.引进记号
![]()
![]() k =
k =![]()
上指标“0”表示偏导数是在x0计算的.定义行列式Di为
Di
对n个变量依次计算n个行列式D1,D2,…,Dn.那末
(i)稳定点x0是极小点的充分条件是:所有的行列式都是正的,即
Di>0, i=1,2,![]()
(ii)稳定点x0是极大点的充分条件是:所有标号为偶数的行列式是正的,所有标号为奇数的行列式是负的,即
Di<0, i=1,3,![]()
Di>0, i=2,4,![]()
如果上列两条件都不满足,那末稳定点可以不是极值点.如果所有的Di都是零,就必须考察更高阶的偏导数.
3.约束条件为等式的条件极值
求函数
y
= f (x), x=(x1,x2![]() )
)
在m(m<n)个约束条件
gk(x)=0, k =1,2,![]()
下的极值.
[直接代入法] 从约束条件的m个方程中将其m个变量解出,用其余n-m个变量表示,然后直接代入函数中去,这样就变为一个求n-m个变量的函数的无约束条件的极值问题.如果从约束方程能够将m个变量解出,这个方法是可行的.
[拉格朗日乘数法] 引进修正的系数
F=y+![]()
式中λk为待定常数.把F当作n+m个变量x1,![]() xn和λ1,λ2,
xn和λ1,λ2,![]() 的无约束的函数,对这些变量求一阶偏导数得稳定点所要满足的方程:
的无约束的函数,对这些变量求一阶偏导数得稳定点所要满足的方程:
![]() , i =1,
, i =1,![]() ,n
,n
gk=0, k =1,2,![]()
例1 求函数
y
=![]()
在约束条件
2x1+3x2=6
下的极值.
解 由于
y
=![]()
和 g =2x1+3x2-6=0
可知修正的函数为
F
= (![]() )+λ(2x1+3x2-6)
)+λ(2x1+3x2-6)
解方程组
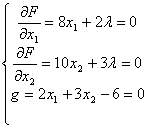
得 λ=![]() ,x1=
,x1=![]() ,x2=
,x2=![]()
所以函数F的稳定点为
x1=![]() , x2=
, x2=![]()
由于
D1=![]() = 8 >0
= 8 >0
D2=![]() =80>0
=80>0
这是一个极小点,函数y的极小值为![]() .
.
[惩罚函数法] 在搜索极小点时引进修正函数
F = y+![]() (1)
(1)
式中Pk是任意大的正整数,![]() 称为惩罚函数.这样就可把问题化为新函数F的无条件极值问题,可以用不断增大Pk的数值来极小化.也可引进如下形式的新函数
称为惩罚函数.这样就可把问题化为新函数F的无条件极值问题,可以用不断增大Pk的数值来极小化.也可引进如下形式的新函数
F
= y+![]()
式中Pk是任意大的正整数.
对搜索极大点时,惩罚函数前取负号,即引进新函数
F
= y-![]()
或 F
= y-![]()
例2 用惩罚函数法解例1.
解 利用方程(1)引进修正函数
F
= y+P(g)2=![]()
解方程组
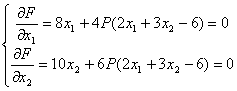
得 x1=![]() x2,x2=
x2,x2=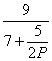
当P很大时,x2趋于![]() ,x1趋于
,x1趋于![]() ,这就是稳定点.由于
,这就是稳定点.由于
D1=![]() =8(1+P)>0
=8(1+P)>0
D2=![]() =16(5+14P)>0
=16(5+14P)>0
所以稳定点是一个极小点,这和例1的结果一致.
4.约束条件为不等式的条件极值
比前面所考虑的更一般的极值问题是求函数
y =f (x),x = (x1,x2,…,xn)
在m个约束条件
gk(x)![]() ,k =1,2,…,m
,k =1,2,…,m
下的极值问题,这里的m不必小于n.
[松弛变量法] 对每一约束不等式都引进一非负的松弛函数Si, 将它变为等式:
![]() =gi+Si=0
=gi+Si=0
每一松弛函数Si仅依赖于一个松弛变量xn+i,一般取
Si=![]()
引进松弛函数后就把问题化为约束条件是等式的极值问题,前面的方法就可以应用了.
例3 求函数
y
=![]()
在约束条件
x1![]()
下的极值.
解 约束条件可写为
g1=1- x1![]()
利用松弛函数S1(x3)可将这个不等式约束化为等式
![]() =g1+S1=
=g1+S1=![]() x1+
x1+![]() =0
=0
利用直接代入法可在函数y中将x1消去得到
y=4(1+![]() )2+5
)2+5![]()
这是一个无约束问题.
稳定点是x2=0,x3=0,所以x1=1.由于
D1=![]() =10>0
=10>0
D2=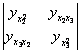 =
=![]() =160>0
=160>0
所以稳定点是修改后的以及原来的函数的极小点,其极小值为4.
[拉格朗日乘数法] 引进松弛函数后,将约束不等式化为等式
![]() =gk+Sk(xn+k)=0, k=1,
=gk+Sk(xn+k)=0, k=1,![]() ,m
,m
同等式约束的情形一样,引进新的目标函数
F=y+![]()
这是一个n+2m个变量的无约束问题.稳定点可以由解下列方程组得到
![]() =0, j=1,
=0, j=1,![]() ,(n+m)
,(n+m)
![]() =0, k=1,
=0, k=1,![]() ,m
,m
以上介绍的多变量函数的极值和条件极值求法中,求稳定点时最后都归结为求实函数方程组
fI
(x1,![]() ,xn)=0, i=1,
,xn)=0, i=1,![]() ,n
,n
的一组实根.有时上列方程组的实根不易求得,要求近似根.关于实根的近似计算法可参考第三章,§4.
十一、微分的应用(II)—曲线的性状与作图
1、曲线的性状及其条件
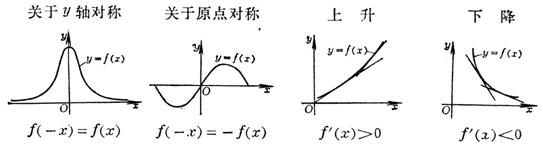
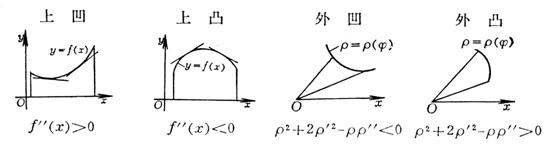
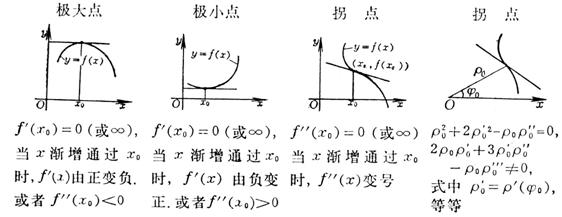
2、奇点
设 P0(x0,y0)是曲线
F(x,y)=0
上的一点,假定函数F(x,y)在点P0有连续的偏导数,并且满足条件
![]() (x0,y0)=0,
(x0,y0)=0,![]() (x0,y0)=0
(x0,y0)=0
则称P0是曲线F(x,y)=0的一个奇点.
如果函数F(x,y)在点P0(x0,y0)的二阶偏导数不全为零,那末称P0为曲线的一个二重点.设
a=![]() ,b=
,b=![]() ,c=
,c=![]()
则根据判别式![]() 的符号在二重点中又可分出如下几种类型的奇点.
的符号在二重点中又可分出如下几种类型的奇点.
|
名称与图形 |
条件与性质 |
举 例 |
||||
|
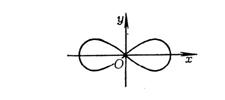
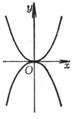
结点
|
(i) (ii)曲线有两支通过点P0,且具有不同切线 |
双纽线
是以原点(0,0)为其结点
|
||||
|
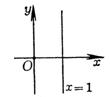
孤立点
|
(i) (ii)在点P0的充分小的邻域里,除了点P0外,没有曲线上其他的点.
|
曲线
的轨迹是由直线x=1和原点(0,0)组成的,原点就是它的一个孤立点 |
|
|||
|
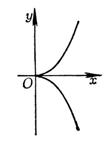
第一种尖点
名称与图形 |
(i) (ii)曲线由两支组成,在点P0有公共切线,这两支在其公共法线的同侧,而在公共切线的异侧.
条件与性质 |
半立方抛物线
是以原点(0,0)为其第一种尖点
举 例 |
|
|||
|
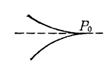
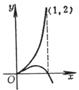
第二种尖点
|
(i) (ii)曲线由两支组成,在点P0有公共切线,这两支在其公共法线的同侧,又在公共切线的同侧. |
曲线
在原点的邻近有两支,即
它们在原点有公共切线,由于0<x<1,y总取正值,所以曲线在原点的邻近的两支都在公共切线和法线的同侧
|
|
|||
|
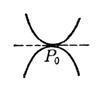
自切点
|
(i) (ii)曲线由两支组成,而彼此在点P0相切 |
曲线
由两条抛物线
组成,它们在原点彼此相切
|
|
|||
如果曲线由参数方程
x = x(t), y = y(t)
|
图5.9 |
表示,那末当![]() =0,
=0,![]() =0时,由参数t0确定的点(x(t0), y(t0))是曲线的奇点.
=0时,由参数t0确定的点(x(t0), y(t0))是曲线的奇点.
特别,曲线由极坐标方程
![]()
表示,那末当![]() =
=![]() =0时,点(
=0时,点(![]() ,
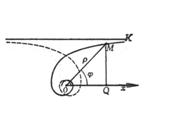
,![]() )是曲线的奇点.例如双曲螺线
)是曲线的奇点.例如双曲螺线![]() 当
当![]() ∞时,
∞时,![]() =0,所以极点是奇点.当极角
=0,所以极点是奇点.当极角![]() 增大到无穷时,曲线上的点无限逼近于极点,但又不能达到(图5.9),所以这种奇点又称为渐近点.
增大到无穷时,曲线上的点无限逼近于极点,但又不能达到(图5.9),所以这种奇点又称为渐近点.
3、 渐近线
曲线存在渐近线的条件及渐近线方程
|
曲线方程 |
条 件 |
渐进线方程 |
|
F(x,y)=0 |
将F(x,y)的最高次数各项之和用 x=
将y = kx+b代入F(x,y)后按x的幂次展开: F(x,kx+b)= 解联立方程
得到k,b,即为渐近线的斜率和纵截距 |
x = a y = b
y=kx+b |
|
y=f (x) |
|
y=kx+b
x=a y=b |
|
|
|
y=kx+b
x=a
y=b |
|
|
|
|
4、作图
作函数
y = f(x)
的图形的步骤大致有以下几点:
(1) 确定自变量x的改变区间,讨论函数的一些基本性质,如奇偶性、对称性和周期性等;
(2)确定曲线与坐标轴的交点;
(3)确定曲线的顶点(极大点、极小点);
(4)确定曲线的凸部,凹部与拐点;
(5)确定曲线的渐近线;
(6)描点作图.
当然,具体问题要具体分析,以上几点不一定都要讨论.
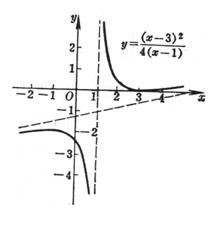
例 画曲线
y=![]()
(1) x可以在区间(-∞,∞)上改变,不对称,也无奇偶性和周期性.
(2)
让x=0,得到y=![]() ;让y=0,得到x=3;就是,曲线与坐标轴交于点(0,
;让y=0,得到x=3;就是,曲线与坐标轴交于点(0,![]() ),(3,0) (图5.10).
),(3,0) (图5.10).
(3)
求出一阶与二阶导数![]() ,
,![]() ,得到顶点(3,0)(极小点)和
,得到顶点(3,0)(极小点)和
(-1,-2)(极大点).
(4)
二阶导数当x>1时为正,当x<1时为负.因此,在区间(1, ∞)内曲线是凹的,在区间(-∞,1)内曲线是凸的.因为![]() 只当x=1时变号,而x的这个值对应于一条平行于y轴的渐近线,所以没有拐点.
只当x=1时变号,而x的这个值对应于一条平行于y轴的渐近线,所以没有拐点.
(5) 当x=1时,y成为无穷大,于是这曲线有一条渐近线x=1.
再求不平行于y轴的渐近线.
|
图5.10 |
k=![]()
b=![]()
![]()
所以 y=![]()
是一条不平行于y轴的渐近线.
由这些性质描出曲线(图5.10).